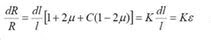TEMA V: SENSORES GENERADORES

Definición de sensores generadores

Se consideran sensores generadores aquellos que generan una señal eléctrica a partir de la magnitud que midan, sin necesidad de una alimentación eléctrica.

Ofrecen una alternativa para medir muchas de las magnitudes ordinarias, sobre todo temperatura, fuerza y magnitudes afines. Pero, además, dado que se basa en efecto reversible, están relacionados con diversos tipos de accionadores o aplicaciones inversas en general. Es decir, pueden emplear para la generación de acciones no eléctricas a partir de señales eléctricas.

¿Qué es efecto reversible?

Se define como aquel proceso que una vez ocurrido puede ser revertido a su estado inicial, sin producir cambios en el sistema o sus alrededores. En otras palabras el sistema y alrededores retornan a su estado original sin sufrir variaciones. Los procesos reversibles son idealizaciones de procesos verdaderos.

¿Qué es efecto irreversible?

Es aquél que supone la imposibilidad, o la dificultad extrema, de retornar a la situación anterior a la acción que lo produce.

¿Qué es efecto termoeléctrico?

El efecto termoeléctrico en un material relaciona el flujo de calor que lo recorre con la corriente eléctrica que lo atraviesa. Este efecto es la base de las aplicaciones de refrigeración y de generación de electricidad: un material termoeléctrico permite transformar directamente el calor en electricidad, o bien generar frío cuando se le aplica una corriente eléctrica.

El primer efecto termoeléctrico fue descubierto por el físico alemán Thomas Johann Seebeck en 1821. Seebeck se dio cuenta de que una aguja metálica es desviada cuando se la sitúa entre dos conductores de materiales distintos unidos por uno de sus extremos y sometidos a una diferencia de temperatura (véase Efecto Seebeck). Este efecto es de origen eléctrico, ya que al unir dos materiales distintos y someterlos a una diferencia de temperatura aparece una diferencia de potencial. La principal aplicación práctica del efecto Seebeck es la medida de temperatura mediante termopares.Unos años más tarde, en 1834, el físico francés Jean-Charles Peltier descubrió el segundo efecto termoeléctrico: en la unión de dos materiales diferentes sometidos a una corriente eléctrica aparece una diferencia de temperaturas (véase Efecto Peltier).El físico inglés William Thomson (Lord Kelvin) demuestra en 1851 que los efectos Seebeck y Peltier están relacionados: un material sometido a un gradiente de temperatura y recorrido por una corriente eléctrica intercambia calor con el medio exterior. Recíprocamente, un material sometido a un gradiente de temperatura y recorrido por un flujo de calor genera una corriente eléctrica. La diferencia fundamental entre los efectos Seebeck y Peltier considerados por separado y el efecto Thomson es la existencia de este último en un único material, sin necesidad de que exista una unión entre materiales distintos.

2 Tipos:

a) Reversibles: Efecto Peltier.Efecto Thompson.

b) Irreversibles: Efecto Joule.

Defina con texto y con gráficos el Efecto Peltier

El efecto Peltier consiste en el calentamiento o enfriamiento de la unión entre dos metales al pasar una corriente por ella (figura). Ocurre que si se invierte el sentido de la corriente, se invierte también el sentido del flujo de calor, es decir, si una unión antes se calentaba, al cambiar el sentido de la corriente se enfriará. Además, este efecto tiene un comportamiento lineal que viene dado por el coeficiente Peltier, πAB, que representa el calor generado en la unión entre A y B por unidad de corriente que circula de B a A.

Y para una unión a temperatura absoluta T, se demuestra que

Defina con texto y con gráficos el Efecto Thompson

El efecto Thomson consiste en la absorción o liberación de calor por parte de un conductor eléctrico homogéneo, con una distribución de temperaturas no homogénea, por el que circula una corriente [Biel J. G., 1997].

El flujo neto de potencia calorífica por unidad de volumen, en un conductor de resistividad r, con un gradiente longitudinal de temperatura, por el que circula una densidad de corriente J será:

donde s es el coeficiente Thomson. El primer término corresponde al efecto Joule, irreversible, mientras que el segundo expresa el efecto Thomson, reversible. Desarrollando esta expresión para obtener la relación entre el coeficiente Thomson y Seebeck y teniendo en cuenta las ecuaciones que rigen los efectos Peltier y Seebeck, se llega a

Quedando para la unión:

Defina con texto y con gráficos el Efecto Seebeck

El efecto Seebeck puede explicarse en términos de la teoría de electrones libres en metales. Según esta aproximación, los electrones en un metal se mueven al azar, sin sufrir el efecto de fuerza neta alguna, al estar rodeados por otros iones en forma simétrica.

Cerca de la superficie del material, empero, la situación es diferente, debido a la rotura de la simetría. Si ahora se colocan dos materiales formando una juntura, la diferencia en densidades electrónicas a ambos lados de la interface se traduce en una fuerza neta sobre los electrones, que tienden a moverse del material con mayor densidad a aquel con menos. Este flujo de electrones induce la aparición de un campo eléctrico y consecuentemente de una diferencia de potencial en la juntura.

Consideremos ahora un circuito formado por dos de estas junturas puestas en serie, en lo que comúnmente se denomina una termocupla. Si la temperatura de las dos junturas que conforman la termocupla es la misma, los campos eléctricos formados en cada juntura tendrán igual módulo, pero signos distintos, por lo que la diferencia de potencial a lo largo de todo el circuito será nula.

Si por otro lado, una de las junturas está a mayor temperatura, los electrones de la juntura más caliente vibrarán más y el campo eléctrico generado en esta juntura será distinto (mayor) al generado en la juntura a menor temperatura.

De esta manera, la diferencia de temperaturas entre las junturas se evidencia como una diferencia de potencial en el circuito.

Tipos de Termopares

En las uniones de termopar interesa tener: resistividad elevada para tener una resistencia alta sin requerir mucha masa, lo cual implicaría alta capacidad calorífica y respuesta lenta; coeficiente de temperatura débil en la resistividad; resistencia a la oxidación a temperaturas altas, pues debe tolerar la atmósfera donde van a estar, y linealidad lo mayor posible.

Para lograr estas propiedades se emplean aleaciones especiales: níquel (90)/cromo (10) -cromel-; cobre (57)/ níquel (43); níquel (94)/aluminio (2)/manganeso (3)/silicio (1) -alumel-; etc. La protección frente al ambiente se logra mediante una capsula, normalmente de acero inoxidable. La velocidad de respuesta y la robustez de la sonda vendrán afectadas por el espesor de dicha vaina. El silicio y el germanio presentan también propiedades termoeléctricas, si bien hasta ahora han encontrado más aplicación como refrigeradores (elementos Peltier) que como temopares de medida. En el cuadro se recogen las características de algunos de los termopares más comunes y su designación de acuerdo con las normas ANSI.

Para medir la temperatura de superficies, hay modelos fabricados con tecnología de capa fina.

Termopares más comunes

Los termopares J son versátiles y de bajo coste. Se pueden emplear en atmósferas oxidantes y reductoras. Se aplican a menudo en hornos de combustión abiertos a la atmósfera. Los termopares K se emplean en atmósferas no reductoras y, en su margen de medida, son mejores que los de tipo E, J y T cuando se trata de medir en atmósfera oxidantes. Los termopares T resisten la corrosión, de modo que se pueden emplear en atmósferas de alta humedad. Los termopares E son los de mayor sensibilidad y resisten la corrosión por debajo de 0°C y las atmósferas oxidantes. Los termopares N resisten la oxidación y ofrecen mejor estabilidad a altas temperaturas. Los termopares con metales nobles (B, R y S) tienen muy alta resistencia a la oxidación y a la corrosión.

Los tipos de termopares los podemos identificar con un código de colores, el cual varia dependiendo del país del fabricante

Construcción de Termopares

Según la aplicación, se dispone de distintos tipos de uniones:


Distintos tipos de uniones de termopar y sus vainas.
a) unión soldada en extremos
b) unión soldada en paralelo
c) hilo trenzado
d) termopar expuesto: respuesta rápida
e) termopar encapsulado: aislamiento eléctrico y ambiental
f) termopar unido a la cubierta: aislamiento ambiental

Las uniones desnudas se emplean para medidas estáticas, pero son frágiles, o de flujos de gases no corrosivos donde se requiere un tiempo de respuesta rápido. Las uniones aisladas se emplean para medir en ambientes corrosivos donde además interese aislamiento eléctrico del termopar. Éste queda entonces encerrado por la vaina y aislado de ésta por un buen conductor térmico como el aceite, mercurio o polvo metálico. Si se desea respuesta rápida y no hace falta una vaina gruesa. se emplean aislantes minerales como polvo de MgO, Al2 O3 o BeO. Según el grado de compactación del aislante, la respuesta final es más o menos lenta y la temperatura máxima soportada es también distinta. Los termopares aislados también se aplican en medidas a alta presión.

Mediante uniones puestas a masa, se pueden medir temperaturas estáticas o de flujos de gases o líquidos corrosivos y, como la unión está soldada a la vaina protectora, la respuesta térmica es más rápida. Pero si la masa es ruidosa, no sirve y hay que aislar térmicamente el termopar. Además, la mayor masa del sensor implica un mayor error por conducción térmica.

Normas de aplicación practica por los Termopares

La medición de temperaturas mediante termopares, además de las ventajas e inconvenientes expuestos esta sujeta a una serie de leyes verificadas experimentalmente, que simplifican en gran manera el análisis de circuitos con termopares.

• Ley de los circuitos homogéneos

En un circuito de un único metal homogéneo no se puede mantener una corriente termoeléctrica mediante la aplicación exclusiva de calor aunque se varíe la sección transversal del conductor.

En la Figura anterior las temperaturas T3 y T 4 no cambian la energía termo electromotriz (ftem) debida a T1 y T2 en particular, si T1 es igual a T2 y se calientan A ó B no fluye corriente alguna.

Es decir en otras palabras las temperaturas intermedias a las que puede estar sometido cada conductor no altera la ftem. Tampoco ocurre esto debido a una determinada diferencia de temperaturas entre las uniones Sin embargo, esto no significa que si hay distintas temperaturas a lo largo de un circuito se tengan que emplear necesariamente hilos de extensión largos iguales a los del termopar. Para esto se emplean los denominados cables de compensación, los cuales son de metales que, siendo más económicos que los de termopares utilizados frecuentemente en la industria no presentan ftem. significativas

• Ley de los Metales Intermedios

La suma algebraica de las ftem en un circuito compuesto de un número cualesquiera de metales distintos es cero. Si todo el circuito está a una temperatura uniforme.Esto significa que se puede intercalar un instrumento de medida, sin añadir errores, siempre y cuando las nuevas uniones estén a la misma temperatura. El instrumento se puede intercalar en un conductor o en un a unión. Un colorario de estas leyes que si se conoce la relación térmica de dos metales distintos con un tercero. Se puede encontrar la relación entre los dos primeros. Por lo tanto no hace falta calibrar todos los posibles pares de metales para conocer la temperatura correspondiente a 1a ftem. detectada con un par determinado. Basta con conocer su comportamiento con un tercero. Se ha convenido en tomar el Platino como referencia.

• Ley de las temperaturas sucesivas o intermedias

Si dos metales homogéneos producen un ftem. E1 cuando las uniones están a T1 y T2 y una ftem.E2, cuando las uniones están a T2 y T3, la ftem. cuando las uniones estén a T1 y T3 será (E1 + E2).Esto significa, por ejemplo, que la unión de referencia no tiene porque estar a ooc si no que puede usarse otra temperatura de referencia.

En el caso (a) se trata de la conexión serie de varios termopares, constituyendo lo que se denomina una termopila. Es fácil comprobar que aumenta la sensibilidad respecto al caso de un soto termopar. En el caso (b) la conexión es en paralelo, y se detecta la temperatura media si todos los termopares son lineales en el margen de medida y tiene la misma resistencia.

Efecto de la temperatura ambiente en la unión de referencia de los termopares

Un termopar convencional con un tubo de protección metálico se encuentra sometido a una diferencia de temperatura, pues una parte de él está en contacto con el proceso y la otra extremidad en contacto con el ambiente, cada una de ellas a cierta temperatura. Es inevitable, por tanto, que por el conjunto sensor/tubo de protección exista un flujo de calor que parte de la región de mayor temperatura hacia la de menor temperatura. El equilibrio ocurre cuando el flujo de calor recibido por el sensor es igual al que se ha perdido, por lo que en tal situación su temperatura no es necesariamente igual a la temperatura del proceso.

Compensación de la unión de referencia en circuitos de termopares

Para aplicar el efecto Seebeck a la medida de temperaturas, es necesario mantener una de las uniones a una temperatura de referencia. Una solución consiste en disponer la unión de referencia en hielo fundente. Es una solución de gran exactitud y facilidad de montaje, pero es de difícil mantenimiento y coste alto. Se puede mantener también la unión de referencia a una temperatura constante a base de emplear un refrigerador Peltier o un horno termostatado. Pero, en cualquier caso, debe usarse mucho hilo de uno de los dos metales del termopar, y esto encarece la solución.

La solución de la figura anterior permite emplear un hilo de conexión más económico (cobre), si bien sigue siendo una solución cara por la necesidad de mantener una temperatura de referencia constante. Si el margen de variación de la temperatura ambiente es menor que la resolución deseada, puede dejarse la unión de referencia simplemente al aire. En caso contrario, se emplea la denominada compensación electrónica de la unión de referencia. Se procede de la siguiente forma:

Compensación electrónica de la unión de referencia en un circuito de termopares: se miden las variaciones de temperatura ambiente con otro sensor y se suma una tensión igual a la generada en la unión fría.

Consiste en dejar que la unión de referencia sufra las variaciones de la temperatura ambiente, pero éstas se detectan con otro sensor de temperatura, dispuesto en la vecindad de la unión de referencia, y se suma una tensión igual a la generada en la unión fría. La tensión de alimentación del puente debe ser estable y puede ser, por ejemplo, la de una pila de mercurio o la de un generador electrónico de una tensión de e referencia estable. Hay circuitos integrados que miden la temperatura ambiente y ofrecen una tensión de compensación para distintos termopares. El LT1025 se puede aplicar a termopares E, J, D, R, S y T. Los AD594 y AD595 integran, además de la compensación (para termopares J y K, respectivamente), un amplificador de instrumentación.

Explicación de la tabla estándar de termopares

Los termopares comerciales se designan por letras (T, E, J, K, R) que identifican los materiales que contienen y se especifican generalmente por su sensibilidad o coeficiente térmico (MV/ºC).

El tipo E, J, K, y T son termopares de base metálica y se pueden utilizar hasta por encima de 1000°C. El tipo S, R, y B se denominan termopares nobles por poseer platino como elemento básico y se pueden utilizar hasta por encima de 2000°C.

Termopar tipo T (Cu- Constantan)
Termoelemento positivo: Cu 100%
Termoelemento negativo: Cu55%, Ni45%
Rango de utilización: -270ºC a 400ºC
F.E.M. producida: -6,258 mV a 20,872 mV
Características: puede utilizarse en atmósferas inertes, oxidables o reductoras. Gracias a la gran homogeneidad con que el cobre puede ser procesado, se obtiene una buena precisión. En temperaturas superiores a 300ºC, la oxidación del cobre se torna muy intensa, lo que reduce su vida útil y ocasiona desvíos en la curva de respuesta original.

Termopar tipo J (Fe- Constantan)
Termoelemento positivo: Fe99,5%
Termolemento negativo: Cu55%, Ni45%
Rango de utilización: -210ºC a 760ºC
F.E.M. producida: -8,096 mV a 42,919 mV
Características: puede utilizarse en atmósferas neutras, oxidables o reductoras. No se recomienda en atmósferas muy húmedas y a bajas temperaturas el termoelemento positivo se vuelve quebradizo. Por encima de 540ºC el hierro se oxida rápidamente. No se recomienda en atmósferas sulfurosas por encima de 500ºC.

Termopar tipo E (Cr- Constantan)
Termoelemento positivo: Ni90%, Cr10%
Termolemento negativo: Cu55%, Ni45%
Rango de utilización: -270ºC a 1000ºC
F.E.M. producida: -9,835 mV a 76,373 mV
Características: Puede utilizarse en atmósferas oxidables, inertes o al vacío, no debe utilizarse en atmósferas alternadamente oxidables y reductoras. Dentro de los termopares a menudo utilizados, es el que posee mayor potencia termoeléctrica, bastante conveniente cuando se desea detectar pequeñas variaciones de temperatura.

Termopar tipo K (Cr- Constantan)
Termoelemento positivo: Ni90%, Cr10%
Termoelemento negativo: Ni95%, Mn2%, Si1%, Al 2%
Rango de utilización: -270ºC a 1200ºC
F.E.M. producida: -6,458 mV a 48,838 mV
Características: Puede utilizarse en atmósferas inertes y oxidables. Por su alta resistencia a la oxidación se utiliza en temperaturas superiores a 600ºC y en algunas ocasiones en temperaturas por debajo de 0ºC. No debe utilizarse en atmósferas reductoras y sulfurosas. En temperaturas muy altas y atmósferas pobres en oxigeno ocurre una difusión del cromo, lo que ocasiona grandes desvíos de la curva de respuesta del termopar. Este último efecto se llama “green - root”.

Termopar tipo N (Nicrosil - Nisil)
Termoelemento positivo: Ni84,4%, Cr14,2%, Si1,4%
Termoelemento negativo: Ni95,45% Si4,40%, Mg0,15%
Rango de utilización: -270ºC a 1300ºC
F.E.M. producida: -4,345 mV a 47,513 mV
Características: Este nuevo tipo de termopar es un sustituto del termopar tipo K que posee una resistencia a la oxidación superior a éste. En muchos casos también es un sustituto de los termopares a base de platino a raíz de su temperatura máxima de utilización. Se recomienda para atmósferas oxidables, inertes o pobres en oxígeno, ya que no sufre el efecto “green - root”. No debe exponerse a atmósferas sulfurosas.

Termopar tipo S
Termoelemento positivo: Pt90%, Rh10%
Termoelemento negativo: Pt100%
Rango de utilización: -50ºC a 1768ºC
F.E.M. producida: -0,236 mV a 18,693 mV
Características: Puede utilizarse en atmósferas inertes y oxidables, presenta estabilidad a lo largo del tiempo en temperaturas elevadas, superiores a las de los termopares no constituidos de platino. Sus termoelementos no deben exponerse a atmósferas reductoras o con vapores metálicos. Nunca deben insertarse directamente en tubos de protección metálicos, pero sí en tubos con protección de cerámica. Fabricado con alúmina (Al2O3) de alto contenido de pureza. Para temperaturas superiores a 1500ºC se utilizan tubos de protección de platino. No se recomienda el uso de los termopares de platino en temperaturas abajo de 0ºC debido a la inestabilidad en la respuesta del sensor. En temperaturas por encima de 1400ºC ocurre crecimiento de granulaciones que los dejan quebradizos.

Termopar tipo R
Termoelemento positivo: Pt87%, Rh13%
Termoelemento negativo: Pt100%
Rango de utilización: -50ºC a 1768ºC
F.E.M. producida: -0,226 mV a 21,101 mV
Características: Posee las mismas características del termopar tipo "S", aunque en algunos casos es preferible el tipo "R" por tener una potencia termoeléctrica mayor en un11%.

Termopar tipo B
Termoelemento positivo: Pt70,4%, Rh29,6%
Termoelemento negativo: Pt93,9%, Rh6,1%
Rango de utilización: 0ºC a 1820ºC
F.E.M. producida: 0,000 mV a 13820 mV
Características: Puede ser utilizado en atmósferas oxidables, inertes y por un corto espacio de tiempo en el vacío. Normalmente se utiliza en temperaturas superiores a 1400ºC, por presentar menor difusión de rodios que los tipos S y R. A temperaturas abajo de los 50ºC la fuerza electromotriz termoeléctrica generada es muy pequeña

Sensores piezoeléctricos

El efecto piezoeléctrico consiste en la aparición de una polarización eléctrica en un material al deformarse bajo la acción de un esfuerzo.

Es un efecto reversible, de modo que al aplicar una diferencia de potencial eléctrico a un materialpiezoeléctrico, aparece una deformación. Todos los materiales ferroeléctricos son piezoeléctricos. La propiedad piezoeléctrica está relacionada con la estructura cristalina. Estos fenómenos fueron descubiertos por Jacques y Pierre Curie en 1880.

Aplicaciones

La aplicación del efecto piezoeléctrico está sujeto a una serie de limitaciones.

- La resistencia eléctrica que presentan los materiales piezoeléctricos aunque es muy grande no es infinita. De modo que al aplicar un esfuerzo constante se genera inicialmente una carga que inevitablemente es drenada al cabo de un tiempo. Por lo tanto, no tienen respuesta en continua.

- Estos sensores presentan un pico en la respuesta para la frecuencia de resonancia. Por tanto, espreciso trabajar siempre a frecuencias muy inferiores a la de resonancia mecánica.

- La sensibilidad presenta derivas con la temperatura. Además, por encima de la temperatura de Curie (específica para cada material) desaparece el efecto piezoeléctrico.

- La impedancia de salida de estos sensores es muy alta, por lo que para medir la tensión de salida es preciso utilizar amplificadores con una impedancia de entrada enorme. Son los denominados amplificadores electrométricos o de carga.

Entre las ventajas de los sensores piezoeléctricos destacaremos las siguientes:

- Alta sensibilidad, obtenida muchas veces a bajo coste.

- Alta rigidez mecánica; las deformaciones experimentadas son inferiores a 1μm. Esta alta impedancia mecánica es conveniente para la medida de variables esfuerzo (fuerza, presión, etc)

- Pequeño tamaño y posibilidad de obtener dispositivos con sensibilidad unidireccional. Estas características hacen a este tipo de sensores especialmente adecuados para medir todo tipo de vibraciones. Por ejemplo una aplicación típica es como micrófono. También se utilizan mucho en la detección por ultrasonidos.

Sensores piroeléctricos

El sensor piroeléctrico esta hecho de un material cristalino que genera una pequeña carga eléctrica cuando es expuesto al calor en forma de radiación infrarroja. Cuando la cantidad de radiación es notable el cristal cambia, la cantidad de carga también cambia y puede entonces ser medida con un sensible dispositivo FET construido dentro del sensor. Los elementos del sensor son sensibles a la radiación en un amplio rango entonces se agrega una ventana que actúa como filtro para limitar la radiación de llegada a un rango de 8 a 14 micras donde es mas sensible a la radiación del cuerpo humano.

Sensores fotoeléctricos

Efecto fotovoltaico

El efecto fotoeléctrico interno visto para los fotoconductores, cuando se produce en la zona de una unión p-n permite obtener una tensión eléctrica que es función de la intensidad de la radiación incidente. A la generación de un potencial cuando una radiación ioniza una zona donde hay una barrera de potencial se la denomina efecto fotovoltaico.Al poner en contacto un semiconductor p (dopado con aceptadores) con un semiconductor n (dopado con donadores), debido al movimiento térmico hay electrones que pasan a la zona p y “huecos” que pasan a la zona n, donde se recombinan, respectivamente, con los portadores de carga de signo, como resultado, en una pequeña zona a ambos lados de la superficie de contactos apenas hay portadores libres, y los iones positivos de la zona n y los negativos de la zona p, fijos en sus posiciones en la estructura cristalina, crean un intenso campo eléctrico que se opone a la difusión de más portadores a través de esta barrera de potencial. De este modo se llega a un equilibrio entre la corriente de difusión y la inducida por este campo eléctrico. Si se dispone una conexión externa con cada semiconductor, no se detecta diferencia de potencial interna en la unión queda compensada exactamente por los potenciales de contacto de las conexiones externas con el semiconductor.

Materiales y aplicaciones

Aunque existen formas adicionales a la unión p-n para crear una barrera de potencial, ésta es la más frecuente en sensores. Si la unión p-n está constituida por un mismo semiconductor, se habla de homounión. En caso contrario, se trata de una heteruounión. En la elección del material hay que tener en cuenta la longitud de onda de la radiación a detectar. En la zona visible y del infrarrojo cercano se emplean el silicio y el selenio, el primero en forma de homouniones, mientras que el segundo consta de una capa de selenio (p) sobre óxido de cadmio (n). Al silicio se añade a veces una zona de silicio intrínseco (no dopado) entre las zonas p y n. Esto aumenta la anchura de la zona desierta y repercute en un mayor rendimiento a longitudes de onda largas, así como en una mayor rapidez y menor ruido y corriente de oscuridad. Para otras longitudes de onda se emplean el germanio, antimoniuro de indio, arseniuro de indio, etc.

TEMA II: SENSORES MODULADORES

Los sensores moduladores son aquellos que varían un parámetro eléctrico en función de la variable a medir. La variable puede ser presión, temperatura, caudal, etc., y el parámetro eléctricopuede ser resistencia, inductancia, capacitancia o campo magnético o eléctrico. La clasificación general de esto sensores se hace en Sensores resistivos y sensores de reactancia variable.

1. Sensores resistivos.

Los sensores basados en la variación de la resistencia eléctrica de un dispositivo son probablemente los más abundantes. Ello se debe a que son muchas las magnitudes físicas que afectan al valor de la resistencia eléctrica de un material.

Para la clasificación de los diversos sensores de esta clase se ha tomado como criterio la magnitud física medida. El orden seguido es:

· Variables mecánicas
· Variables térmicas
· Variables magnéticas
· Variables ópticas
· Variables químicas

1.1. Potenciómetros (Variables mecánicas)

Un potenciómetro es un resistor al que le puede variar el valor de su resistencia. De esta manera, indirectamente se puede controlar la intensidad de corriente que hay por una línea si se conecta en serie, o la diferencia de potencial de hacerlo en paralelo.

El potenciómetro posee un contacto móvil que se desliza o gira, y la resistencia entre este contacto móvil y uno de los terminales fijos es:

1.2. Galgas extensométricas (Variables mecánicas)

Las galgas extensométricas son sensores de deformaciones basados en la variación de la resistencia eléctrica con la deformación, en un hilo conductor calibrado, o en resistencias construidas a base de pistas de semiconductor. Se emplean también, combinadas con muelles o piezas deformables para detectar de forma indirecta esfuerzos. En definitiva suelen usarse más que como sensores de deformación como sensores de medida indirecta de esfuerzos (fuerza o par).

En las galgas de hilo la resistencia esta formada por un hilo dispuesto en forma de zigzag sobre un soporte elástico, con una longitud preferente (L) a lo largo de la cual se encuentra la mayor cantidad de hilo . Al deformarse la galga en la dirección preferente, se produce un alargamiento del hilo y una disminución de su sección y, por tanto, una variación en su resistencia. Para poder medir variaciones de resistencia significativas, la galga debe tener una resistencia alta 100 y 1000, y funcionar con un consumo muy bajo, para evitar que el efecto Joule provoque variaciones importantes de la resistencia por calentamiento. La medida de deformaciones requiere una meticulosa colocación de las galgas y una calibración laboriosa, y la amplificación suele realizarse por métodos diferenciales con tres hilos.

1.3. Galgas extensométricas (Variables mecánicas)

Se basan en la variación de la resistencia de un conductor cuando se le somete a un esfuerzo mecánico. Sea un hilo metálico de resistencia R:

cualquier esfuerzo al que se le someta provocará un cambio de resistencia que se deberá al cambio de alguno de los parámetros:

Según la Ley de Hooke, si aplicamos una fuerza F sobre un conductor unidimensional, el cambio de longitud que experimenta cumplirá que:

donde E es una constante del material denominada módulo de Young, σ es la tensión mecánica y ε es la deformación unitaria. La deformación unitaria es adimensional, pero suele hablarse de microdeformaciones (1 microdeformación = 1 με = 10-6 m/m). Si se considera que el material tiene una determinada dimensión transversal t, es evidente que una deformación longitudinal provocará también una deformación transversal. Se cumple que:

donde μ es el coeficiente de Poisson. Si consideramos que el hilo tiene una sección transversal circular de diámetro t, se tendrá que:

donde C es la constante de Bridgman. Dado que hemos considerado el conductor con una sección circular y una longitud l, su volumen será:

Con todo lo anterior, nos queda:

y la resistencia de la galga puede expresarse como:

siendo R0 la resistencia en reposo x = Kε.

Los principales problemas de las galgas son:

· Cuidar el margen elástico.
· El esfuerzo debe ser totalmente transversal a la galga.
· La temperatura altera su valor.

Las galgas se pueden aplicar a:

· Medida de fuerza.
· Medida de presión.
· Medida de desplazamientos pequeños.
· Medida de vibración.

1.4. Termorresistencias (Variable térmicas)

Las termorresistencias son resistores variables con la temperatura, pero no están basados en conductores como los RTD, sino en materiales semiconductores. Si su coeficiente de temperatura es negativo se denominan NTC (Negative Temperature Coefficient), mientras que si es positivo se denominan PTC (Positive Temperature Coefficient).

Los símbolos respectivos son los siguientes, donde el trazo horizontal en el extremo de la línea inclinada indica que tienen un comportamiento no lineal.

El fundamento de los termistores está en la dependencia de la resistencia de los semiconductores con la temperatura, debida a la variación con esta del número de portadores. Al aumentar la temperatura lo hace también el número de portadores reduciéndose la resistencia (coeficiente de temperatura negativo, NTC). Esta dependencia varía con la concentración de impurezas. Si el dopado es muy fuerte, el semiconductor adquiere propiedades metálicas y presenta un coeficiente de temperatura positivo (PTC) en un margen de temperaturas limitado.

1.5. Termistores (Variables térmicas)

Los termistores también son resistencia que varían su magnitud con la temperatura. Se diferencian de las termorresistencia por que están basadas en semiconductores. Por tanto su característica no es lineal, aunque dentro de un margen adecuado pueda ser considerada de es amanera. Su símbolo será:

La raya quebrada indica que no es lineal. El elemento positivo o negativo indica que tiene una característica positiva o negativa respectivamente. Es decir, si es de coeficiente positivo, PTC, la resistencia se incrementa con la temperatura. Si es de coeficiente negativo, NTC, disminuye con la temperatura.

En el caso de una NTC la ecuación característica será

Donde:B = temperatura característica del material (2000 K a 5000 K)R0 = Resistencia a la temperatura de referencia T0, normalmente la temperatura ambiente (25 °C o 298 K)

Tiene como ventajas el ser más sensible que las Termorresistencias, más rápidas y permite hilos de conexión mayores.

Tiene como desventaja el ser no lineal, y al variar su temperatura por el autocalentamiento del material.

1.6. Magnetorresistencias (Variable magnéticas)

Las magnetorresistencias se basan en la variación de resistencia en un conductor por variaciones en el campo magnético. Este efecto se denomina efecto magnetorresistivo y fue descubierto por Lord Kelvin en 1856.

Este tipo de sensores tiene la ventaja con respecto a los sensores inductivos, por ser de orden cero, y con respecto a los sensores de efecto Hall por ser más sensible y proveer un mayor margen de medición de medición.

Está formada por una aleación de Hierro y Níquel (permalloy).

Tiene las siguientes aplicaciones:

Medición de campos magnéticos en las lectoras de tarjetas.
Otras magnitudes que provean un cambio en el campo magnético, como el desplazamiento de una pieza, detectores de proximidad, nivel de flotador, etc. En estos casos se utiliza un imán que cambia su posición con el proceso. El campo generado por el imán es medido por la magnetorresistencia

1.7. Fotorresistencias (Variables ópticas)

Las fotorresistencias o LDR, es un dispositivo que cambia su resistencia por el nivel de incidencia de luz. Está formada por materiales semiconductores. Su símbolo es:

Propiedades:

· Solo componentes con terminales.
· Sensores de diferente tamaño.
· Impermeables o sobre sustrato de cerámica.
· Sensitivos en el espectro visible.

Aplicaciones:

· Control de iluminación.
· Retrovisor de automóvil automático.

1.8. Higrómetros resistivos (Variables químicas)

El higrómetro se utiliza para medir humedad. Se basan en la variación de resistencia que experimentan los materiales por la humedad, como el vapor de agua en un gas o el agua absorbida en un líquido o sólido.

La mayoría de los aislantes eléctricos presentan un descenso brusco de resistividad al aumentar la humedad de su entorno. Si se mide la variación de su resistencia se tiene un higrómetro resistivo. La relación entre la humedad relativa y la resistencia no es lineal, es casi exponencial. La resistencia se debe medir con una corriente alterna de valor medio cero.

1.9. Acondicionamiento: Puente de Wheastone, Amplificador de Instrumentación.

El puente de Wheatstone es un dispositivo orientado a corregir parte del problema que presenta la configuración anterior: Linealidad y sensibilidad. El circuito es el mostrado a continuación.

Donde,

Si en el equilibrio se considera

Entonces,

Se ha obtenido una relación no lineal, lo cual será proporcional solo cuando x <<>

¿Cómo medir la salida de un puente?
· Mediante un galvanómetro, aunque este tiene el problema de su baja resistencia.
· Con un Osciloscopio se tiene le problema que no posee entradas diferenciales.
· Con un Multímetro digital puede resultar muy costoso.

1.8.2 Amplificador de Instrumentación

Se denomina amplificador d instrumentación a aquel dispositivo que tenga simultáneamente alta impedancia de entrada, alto rechazo del modo común, ganancia estable y variable con una sola resistencia, y que no se contraponga ganancia-ancho de banda, tensión y corriente de fugas bajas, bajas derivas, impedancia de salida baja. La estructura típica de un A.I. es la mostrada en la figura siguiente, cuya ecuación es:

Si R4 = R5 = R6 = R7 , entonces,

Con R2 se puede variar la ganancia pero no de forma lineal.

Algunos amplificadores de instrumentación monolíticos son:
· Analog Devices: AD624
· National: LM363
· Burr-Brown: INA101
· Linear: LTC1100, LT1101

Ya que esta estructura es muy típica, algunos fabricantes la ofrecen con redes de resistencias y poder cambiar el valor de la ganancia. El Terminal denominado referencia es accesible en algunas versiones, con el fin de poder desplazar el nivel de tensión de referencia de la salida.

2. Sensores de reactancia variable

Los sensores de reactancia variable tienen las siguientes ventajas con respecto a los resistivos:

· Efecto de carga mínimo o nulo.
· Ideales para la medida de desplazamientos lineales y angulares y para la medida de humedad.
· La no-linealidad intrínseca puede superarse usando sensores diferenciales.

Como limitación tiene que la máxima frecuencia de variación admisible en la variable medida debe ser menor a la frecuencia de la tensión de alimentación empleada.

2.1. Sensores Capacitivos

Los sensores capacitivos pueden detectar materiales conductores y no conductores, en forma líquida o sólida. Existen distintas aplicaciones, incluso control de niveles en depósitos, también para detectar el contenido de contenedores, o en máquinas empaquetadoras. Otras aplicaciones incluyen el posicionado y contaje de materiales en sistemas de transporte y almacenaje, por ejemplo cintas transportadoras y mecanismos de guía.

Los sensores de este tipo pueden ser simples (Co +/- C) y diferenciales (Co + C, Co – C). El caso simple es el condensador variable.

2.1.1. Condensador variable.. PARTE I

Un condensador esta formado por dos placas y un dieléctrico.

Donde,

pero la capacidad C es función de la geometría del conductor, el material del dieléctrico. Por ejemplo, para un condensador de placas planas y paralelas se tiene:

donde ε0 = 8.85 pF/m y εr = ε / ε0ε es la constante dieléctrica del material y ε0 es la constante dieléctrica del vacío

Por tanto, con variar la geometría o el dieléctrico se puede usar para medir un fenómenofísico.

Los problemas que presenta este tipo de medidor es que:

· No se puede despreciar el efecto de los bordes.
· El aislamiento entre placas debe ser alto y constante.
· Existen muchas interferencias capacitivas.
· Los cables de conexión generan condensadores parásitos.

El efecto de bordes es importante ya que en la ecuación de C se indica que esta está afectada por la distancia entre las placas. Realmente está afectada por la distancia que recorren los electrones desde una placa a la otra. Esto es asumiendo que se desplazan perpendicularmente sobre las placas. Pero en la práctica no es así, y ocurre que en los bordes el desplazamiento es angular, recorriendo una distancia mayor. Esto genera un error. Esto se corrige utilizando guardas. La guarda consiste en rodear un o de los electrodos con un anillo puesto al mismo potencial del mismo electrodo.

2.1.1. Condensador variable.. PARTE II

Un condensador esta formado por dos placas y un dieléctrico.
Donde,

C= Q (carga a) / V (dif. De potencial)

pero la capacidad C es función de la geometría del conductor, el material del dieléctrico.

Por ejemplo, para un condensador de placas planas y paralelas se tiene:

C= εo εr A/d (n-1)

donde εo = 8.85 pF/m y εr =  / 0
εr es la constante dieléctrica del material y εo es la constante dieléctrica del vacío.

Por tanto, con variar la geometría o el dieléctrico se puede usar para medir un fenómeno físico.

Los problemas que presenta este tipo de medidor es que:

· No se puede despreciar el efecto de los bordes.
· El aislamiento entre placas debe ser alto y constante.
· Existen muchas interferencias capacitivas.
· Los cables de conexión generan condensadores parásitos.

El efecto de bordes es importante ya que en la ecuación de C se indica que esta está afectada por la distancia entre las placas. Realmente está afectada por la distancia que recorren los electrones desde una placa a la otra. Esto es asumiendo que se desplazan perpendicularmente sobre las placas. Pero en la práctica no es así, y ocurre que en los bordes el desplazamiento es angular, recorriendo una distancia mayor. Esto genera un error.

Esto se corrige utilizando guardas. La guarda consiste en rodear un o de los electrodos con un anillo puesto al mismo potencial del mismo electrodo

Las interferencias capacitivas consiste en que entre cada conductor existen condensadores parásitos. Una solución en este caso es apantallar el cable para llevar todos los posibles contactos a tierra

Otro problema mencionado son los cables de conexión. Al apantallar el cable para reducir las interferencias capacitivas, se introduce un nuevo error, si el cable es largo:; Es la aparición de capacidades en paralelo a lo largo del cable

La linealidad es otro elemento a destacar ya que según sea el parámetro que se tome, podremos obtener una salida directamente proporcional o inversamente proporcional, y por tanto no lineal. Si lo que varía es la distancia d y se mide la admitancia (proporcional a C), la medida sería no lineal. Pero si se mide la impedancia, la medida seria lineal.

El uso de sensores diferenciales permitirá superar esta dificultad.
Otro problema importante es la alta impedancia de salida de este tipo de sensores, determinada por el dieléctrico no conductor utilizado.

Para resolver en este caso existen tres alternativas:

· Colocar la electrónica de acondicionamiento.
· Usar un transformador de impedancia.
· Medir la intensidad de corriente en vez de la tensión.

Es indudable que estos sensores tienen ventajas con respecto a sus homólogos resistivos. Algunas de ellas son:

· Como sensor de desplazamiento tienen un error por carga mecánica casi nulo: sin fricciones, ni histéresis. La fuerza para mover el elemento móvil en un condensador plano es:

F = 1/2 ( εo A/ d² V²)

Para valores reales, la fuerza necesaria para producir un desplazamiento es casi despreciable.
· Estos sensores tienen una estabilidad y reproducibilidad elevadas. C no depende de la conductividad de las placas y por tanto tampoco de la temperatura.
· Se puede obtener una alta resolución, al variar bastante la capacidad. Se puede detectar hasta 10 pm de distancia.

Estos sensores se suelen aplicar para medir desplazamientos. Si el desplazamiento es grande o pequeño, se prefiere utilizar d variable. Si el desplazamiento es intermedio (1-10 cm), se prefiere variar el área de acción entre las placas.

Normalmente la capacidad en estos sensores varía de 500 pF a 1 pF, y se trabaja con frecuencias de 10 kHz para que la impedancia sea pequeña.

Algunas aplicaciones de los sensores son:

· Medida de desplazamientos lineales y angulares.
· Detector de proximidad.
· Cualquier otra magnitud que se pueda convertir en desplazamiento.
· Medidas de nivel de líquido conductor y no conductor.

2.1.2. Condensador diferencial

Condensador diferencial se denomina al formado por tres placas planas paralelas. En general, las placas exteriores suelen ser fijas y la placa central móvil, en respuesta a la variable a detectar. Vemos cómo, a pesar de que C1 y C2 son no lineales, se logra obtener una salida lineal realizando una medida diferencial y con una sensibilidad mayor que en el caso del condensador simple.

Aplicaciones típicas de esta configuración son los micrómetros, acelerómetros e inclinómetros.

Si se disponen las tres placas del condensador diferencial cómo se muestra en la figura derecha y se varía el área entre placas, se tiene que la medida diferencial de la capacidad nos permite obtener una salida lineal con el desplazamiento. Con esta técnica se han llegado a medir desplazamientos de hasta 10-10 mm.

Aunque se ha mejorado en linealidad, el condensador diferencial no esta exento de problemas: dispersión del campo eléctrico en los bordes de los electrodos, aislamiento entre placas, capacidades parásitas, cables de conexión, etc. La dispersión del campo en los bordes de los electrodos puede apreciarse mejor en la figura a. Para evitar este efecto, en la figura b se ha colocado un electrodo de guarda rodeando al electrodo 3. Este electrodo de guarda se mueve junto al electrodo 3 y está puesto a su mismo potencial. Ahora, las líneas de campo aparecen distorsionadas en el borde de la guarda, lo cual no importa ya que no es un electrodo de medida. En cambio el campo si es uniforme en los electrodos de medida. El electrodo de guarda protege simultáneamente al electrodo 3 de campos externos que puedan afectar a la linealidad de la medida.

Aplicaciones de los sensores capacitivos diferenciales:
Estos sensores se utilizan especialmente para medir desplazamientos lineales y angulares.

Este tiene la ventaja de proporcionar mediciones de desplazamiento muy exactas. El circuito necesario para montarlo es similar al puente de wheatstone solo que en lugar de resistencias se usan condensadores. Se debe usar también una capacitancia variable para balancear el circuito.

Este tipo de transductor es útil para medir presión sanguínea, registrar los movimientos de las paredes del pecho, presión plantar, sonidos del corazón y los pulsos radial y braquial. Para lograrlo una de las placas de condensador se mantiene fija, mientras la segunda está unida a un miembro elástico. Una interesante aplicación de los sensores capacitivos la constituyen los capacitares biológicos. Estos utilizan las propiedades dieléctricas del tejido vivo como una parte del capacitor. Cremen (1907) insertó un corazón latiente de rana entre las dos placas de un condensador y registró el cambio de capacitancia cuando el corazón se llenaba y vaciaba de sangre. Un sistema similar fue desarrollado por Joseph (1944) quien colocó el tórax de sujetos humanos, en registro simultáneo con el ECG mostró que los cambios capacitivos estaban asociados con la actividad cardiaca. Para estudiar el flujo sanguíneo Atzler y Lehman (1932) usaron sujetos humanos colocando un electrodo encima del pecho y el segundo en contacto con la espalda. Fening (1936) desarrolló lo que el llamó oscilocapacitógrafo, utilizando una rata que yacía sobre una placa del capacitor, y la otra placa la colocaba 5mm por encima del tórax del animal. Los movimientos respiratorios cambiaban la capacitancia a través de una variación del área, la separación de las placas y la distribución del dieléctrico, cambios que alteraban la corriente del ánodo del tubo oscilador. Así se obtenía un buen registro de la respiración de las ratas. Para una descripción de estos y otros experimentos refiérase al libro de Wilches o Webster.

En general se puede establecer que los sensores capacitivos tienen un pequeño tamaño, construcción robusta y un pequeño desplazamiento volumétrico. La señal de salida es débil por lo que precisan de amplificadores con el riesgo de introducir errores en la medición. Además son sensibles a variaciones de temperatura.

Ventajas
· Simplicidad mecánica
· Error de rozamiento mínimo
· Tamaño y masa pequeños
· Alta resolución y sensibilidad
· Buena reproductibilidad
· Alta estabilidad con la temperatura
· Fácil integración en C.I.

Desventajas
· Resistencias parásitas
· Alta impedancia de salida
· Afectados por campos electromagnéticos
· Necesidad de apantallamiento
· Utilización de guardas

Aplicaciones de estos sensores:
· Desplazamientos lineales y angulares.
· Detector de proximidad.
· Cualquier magnitud que implique un desplazamiento (presión, fuerza, etc)
· Medida de humedad por variación de e.+Medida de Tª (de e=k/(T-Tc)).
· Medida de espesores de materiales dieléctricos.
· Medida de nivel de líquidos.
· Presión, fuerza, par y aceleración
· Deformaciones, galgas capacitivas
· Humedad (óxido de aluminio como dieléctrico)
· Análisis químico
· Nivel de líquidos

2.1.3. Acondicionamiento: divisor de tensión, amplificador de carga, amplificador de transconductancia

Los circuitos de acondicionamiento dependerán de si el sensor es simple o diferencial. Para el caso de condensador simple se tiene.

Divisor de tensión:
El divisor de tensión es un circuito simple que también se aplica para estos sensores.

De aquí se tiene que:

Vs = V (1 + X)/2

si y solo si, Z =Z0

Amplificador de Carga
Un amplificador de carga es un tipo especial de preamplificador que se usa en acelerómetros piezoeléctricos sin circuitos integrados. Su propósito es de convertir la impedancia de salida extremadamente alta del acelerómetro a un valor bajo, adaptado para transmitir la señal de vibración a través de cables a otros instrumentos que la van a procesar. El amplificador de carga es sensible a la cantidad de carga eléctrica generada por el acelerómetro en lugar de al voltaje que genera el mismo. Ya que la carga es independiente del cable conectado al acelerómetro, la sensibilidad del acelerómetro no varía con la longitud del cable como lo hace cuando se usa un amplificador de voltaje.

Un amplificador de transconductancia variable (OTA)
Es un dispositivo electrónico parecido a un amplificador operacional. Si bien en un amplificador operacional, la tensión de salida es proporcional a la tensión de entrada, en un amplificador operacional de transconductancia, es la corriente de salida la que es proporcional a la tensión de entrada:

Esto se consigue con una alta impedancia de salida, a diferencia del amplificador operacional (OA) que presenta una baja impedancia a la salida. Esto implica que el OTA trabajará con bajas corrientes de salida.

OTA´s clásicos son el CA3080 de Harris y el LM13600.Estos circuitos integrados (C.I.) disponen de una entrada de corriente (Amplifier bias input) que controla la ganancia de corriente.

Colocando una resistencia a la salida, se puede hacer la conversión de corriente a tensión, transformando el dispositivo en un amplificador controlado por tensión a través de la referida entrada (amplifier bias input).

La aplicación práctica más común de estos dispositivos es la de amplificador de ganancia variable controlada por tensión (como control de volumen en equipos de audio). Actualmente, para estas aplicaciones existen C.I. de controles de volumen específicos, controlados por una tensión DC o por una señal digital para adecuar un interfaz de un pulsador o de la señal de un mando a distancia.

2.2. Sensores inductivos

Los sensores inductivos son aquellos que producen una modificación de la inductancia o inductancia mutua por variaciones en un campo magnético. Estas variaciones pueden ser fruto de perturbaciones en el campo, o modificación de la distancia de influencia del campo. Solo hablaremos de dos tipos: la reluctancia variable y la inductancia mutua.

2.2.1. Reluctancia variable

Existen ciertos casos donde las condiciones físicas de operación requieren un sensor a prueba de casi todo. La solución acostumbrada son los sensores de reluctancia variable.

Funcionan de la siguiente manera: El campo de un imán permanente es deformado al paso de un objeto de alta reluctancia, como los dientes de un engrane metálico; este cambio en el campo induce un voltaje en una bobina colocada rodeando al imán. La magnitud de este voltaje depende de la velocidad con la que el diente en nuestro ejemplo pasa frente al campo magnético y, cuando es suficientemente grande (4500 mm/seg), puede ser empleado en contadores o indicadores de velocidad directamente.

En nuestro medio usualmente se conocen estos sensores como de "Pick Up" magnético. Y, tienen forma de cilindro metálico, a manera de un tornillo.

Este tipo de sensor se basa en la ley:

Donde φ es el flujo de campo magnético, I es la corriente y N es el número de vueltas del inductor.

Pero el flujo magnético es igual al cociente entre la fuerza magnetomotriz M y la reluctancia magnética R, y además, M = NI, por lo que


Para una bobina de longitud L y sección de área A, donde la longitud sea mucho mayor que el diámetro de las espiras se tiene:

Donde
μr es la permeabilidad relativa del núcleo
L = recorrido de las líneas de campo en el aire.
A = Área de las bobinas.

Normalmente se aprovechan las variaciones de la longitud y de la permeabilidad.

Cuando lo que varía es la distancia L se está hablando de sensores de entrehierro variable, y cuando lo que varia es la permeabilidad se dice que se está hablando de sensores de núcleo móvil.

Esto sensores tiene los siguientes problemas:

· Los campos magnéticos parásitos afectan a L, por lo que se deben apantallar.
· La relación L y R no es constante y varía hacia los extremos.
· L y R son inversamente proporcionales, por lo que las medidas serán normalmente no lineales.
· La temperatura de trabajo debe ser menor a la de Curie del material usado.

Por contra tienen las siguientes ventajas:

· La humedad los afecta muy poco.
· Tiene poca carga mecánica.
· Y una alta sensibilidad.

Algunas configuraciones tipicas se muestran a continuacion: