Se basan en la variación de la resistencia de un conductor cuando se le somete a un esfuerzo mecánico. Sea un hilo metálico de resistencia R:

cualquier esfuerzo al que se le someta provocará un cambio de resistencia que se deberá al cambio de alguno de los parámetros:

Según la Ley de Hooke, si aplicamos una fuerza F sobre un conductor unidimensional, el cambio de longitud que experimenta cumplirá que:
donde E es una constante del material denominada módulo de Young, σ es la tensión mecánica y ε es la deformación unitaria. La deformación unitaria es adimensional, pero suele hablarse de microdeformaciones (1 microdeformación = 1 με = 10-6 m/m). Si se considera que el material tiene una determinada dimensión transversal t, es evidente que una deformación longitudinal provocará también una deformación transversal. Se cumple que:

donde μ es el coeficiente de Poisson. Si consideramos que el hilo tiene una sección transversal circular de diámetro t, se tendrá que:

donde C es la constante de Bridgman. Dado que hemos considerado el conductor con una sección circular y una longitud l, su volumen será:

Con todo lo anterior, nos queda:
y la resistencia de la galga puede expresarse como:
siendo R0 la resistencia en reposo x = Kε.
Los principales problemas de las galgas son:
· Cuidar el margen elástico.
· El esfuerzo debe ser totalmente transversal a la galga.
· La temperatura altera su valor.
Las galgas se pueden aplicar a:
· Medida de fuerza.
· Medida de presión.
· Medida de desplazamientos pequeños.
· Medida de vibración.
Los principales problemas de las galgas son:
· Cuidar el margen elástico.
· El esfuerzo debe ser totalmente transversal a la galga.
· La temperatura altera su valor.
Las galgas se pueden aplicar a:
· Medida de fuerza.
· Medida de presión.
· Medida de desplazamientos pequeños.
· Medida de vibración.

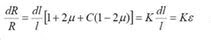

No hay comentarios:
Publicar un comentario